2023年立川高校入試講評　数学

２０２３年の立川高校入試問題　数学で最も難易度が高かった問題は、「３平面図形　問２　証明問題」です。

理由としては２点挙げられます。

①証明内容が「DP+PF＝GH」と線分の長さの和が等しいことを証明する問題

証明問題では珍しい、線分の長さの和が等しいことを証明する問題です。方針を立てるだけでも時間をとってしまう可能性があります。

ポイントはDP＋PFの長さを他の線分の長さで表すことです。また、線分の長さが等しいことは三角形の合同で示すことができます。

②証明の際に補助線を引く

図形問題で一番難しいのが、補助線を引くことです。引き方一つで、図形が大きく変わっていきます。今回は、垂線を引くことで証明が可能となります。

補助線を引くポイントは、垂線や平行な線など特殊な線になることが多いです。先ずは、垂直、平行な線から攻めていければいいと思います。

次に１小問集合問題、２関数問題、４空間図形問題でそれぞれの大問で点数の差が出たと思われる問題を挙げていきます。

１小問集合問題　問２　連立方程式の計算

昨年と同様に分数と小数の混じった連立方程式になります。38/133＝2/7に約分できることに気づけるかがポイントになります。

２関数問題　問２　二等辺三角形になる条件（記述）

記述問題です。場合分けが必要になります。しかし、問題文中に「ＯＢ＝ＡＢの場合を除く」と書いてあることから、場合分けが必要であることが予測できます。

解法には２点間の距離を三平方の定理を利用して解いていきます。座標における２点間の距離を公式化していると、記述スピードは一気に速くなります。

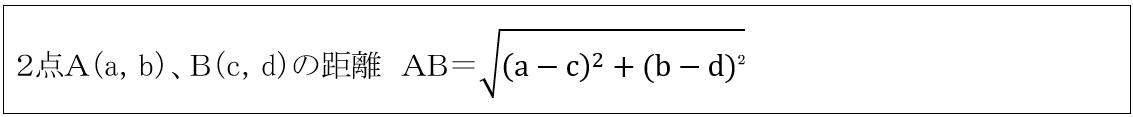
４空間図形問題　問２　条件を満たしているときの線分の長さが等しいことを説明する問題（記述）

記述問題です。この問題ができると、次の問３に繋がり、高得点が狙えます。垂線の長さを求めるので、三平方の定理が使えそうですが、今回は、求めたい線分を立体の高さとみて、体積から方程式をつくり、解いていきます。この解き方は、図形問題でよく使われるので、対応はしやすいと思います。

上記の３問に共通して言えることは、解く問題の難易度が高いわけではなく、計算が複雑で多いということです。複雑な計算を早く、正確にできるように日頃からの計算トレーニングが点数を取れるかどうかのポイントになります。